Har du levd i mer enn et par tiår, har du trolig hørt om år 2000-problemet, eller Y2K, som det gjerne kalles. Du vet, det problemet som endte opp med en forventning blant folk flest om at alle datamaskiner skulle slutte å fungere etter årtusenskiftet. Y2K38 er mye av det samme, men kanskje ikke fullt så enkelt å forstå seg på.
Kort om Y2K
For ryddighetens skyld lønner det seg kanskje å begynne med en kort forklaring av det opprinnelige Y2K-problemet. Det kom kort og godt litt forenklet av at mange datasystemer kun lagret de siste to sifrene i årstallet, dvs. 85 for 1985 og 99 for 1999. Dette førte derimot til at 2000 ble lagret som 00, som igjen ble tolket som 1900. Katastrofespådommer om Y2K nådde temmelig langt ut i befolkningen. Ganske mange forventet tilnærmet total systemsvikt i samtlige datasystemer verden rundt, så fort årstallet rundet 2000. Riktignok ville Y2K forårsaket alvorlige problemer, men konsekvensene var nok en smule mindre enn det mange hadde fått for seg. På grunn av en flerårig iherdig innsats for å løse problemet før det oppstod, ble de aller fleste mulige katastrofene avverget.
Som Y2K… bare verre
Hopp noen år framover i tid, og man flytter fokuset til et nytt og verre problem: Y2K38. Verre både å forstå seg på og å fikse. Y2K38-problemet oppstår nemlig når man lagrer dato og tid som antall sekunder etter 1. januar 1970, med en datatype som på engelsk kalles «signed 32-bit integer». Og her trengs det kanskje en del forklaring, for dette har å gjøre med hvordan datamaskinprogrammer fungerer på et lavt nivå.
Lagring som bits
Når et dataprogram lagrer en verdi i minnet, vil denne verdien ha en datatype. F.eks. om det er en tekststreng, et heltall eller et desimaltall. Dette avgjør hvordan den lagres som bit (ett binært siffer, som er enten 0 eller 1) og byte (dvs. 8 bit) i minnet. For tallverdier er det også delt opp ytterligere i hvor store tall som kan lagres. Størrelsen på tallene vil ganske enkelt variere avhengig av hvor mange bit som brukes til å lagre tallet.
Har man bare 1 bit, kan man bare lagre verdiene 0 og 1. Hvis man har to bit får man det dobbelte, med 4 ulike verdier (0 til og med 3). Har man derimot 32 bit, kan man lagre hele 4 294 967 296 ulike verdier, og den høyeste verdien blir da én mindre enn dette (siden man også må kunne lagre 0). Hvis man i tillegg ønsker å lagre negative tall må den første biten brukes som fortegn. Antall verdier blir da omtrent halvparten. Man vil da kunne lagre tall fra -2 147 483 648 til 2 147 483 647.
For å ikke gjøre lagring i minnet unødvendig komplisert, må «størrelsen» på verdien bestemmes på forhånd når et dataprogram lages. Det vil si, man må velge en passe mengde bit til å lagre det største tallet man vil få behov for. Og dette er hovedårsaken til Y2K38.
Unix-historie og integer overflow
Skaperne av operativsystemfamilien Unix trengte å finne en måte å lagre dato og tid på i operativsystemet. Da tenkte de sannsynligvis at det burde passe bra å bruke antall sekunder siden en bestemt dato. Den datoen endte opp med å være 1. januar 1970 kl. 00:00, sikkert fordi det var den nærmeste relativt runde datoen på den tida. Datoen omtales som «Unix epoch», or har dermed gitt denne formen for tidsregning navnet unixtid («Unix time») eller «Epoch time».

Ved implementering av denne datolagringen, endte man opp med å velge å lagre det som nettopp «signed 32-bit integer». Blant annet i programmeringsspråket C, hvor datatypen som brukes kalles «long», siden den er lengre enn vanlige heltall med 16 bit. «signed 32-bit integer» vil si et 32-bits heltall med fortegn. Fortegnet gjør det mulig å bruke negative verdier for å regne med datoer også før 1970. Men dette betyr altså at eneste gyldige datoverdier er de som tilsvarer heltall fra -2 147 483 648 til 2 147 483 647.
Men hva skjer når antallet sekunder siden 1. januar 1970 overstiger 2 147 483 647, den høyeste verdien som er mulig å lagre som 32 bits heltall med fortegn? Det er nemlig her selve Y2K38-problemet ligger, for nøyaktig 19. januar 2038, klokka 03:13:07, vil denne grensen nås. Da har det gått nøyaktig 2 147 483 647 sekunder siden starten av året 1970. Hva som vil skje neste sekund varierer litt basert på hva slags system det er snakk om. Et sannsynlig utfall er at klokka hopper tilbake til den laveste verdien, -2 147 483 648. Da vil tiden plutselig hoppe til det tidspunktet som er like langt unna 1970 som det 2038 er, noe som tilsvarer 13. desember 1901, klokka 20:45:52. Dette er det tidligste tidspunktet som kan representeres med 32 bit.
Når tallet blir for høyt…
Grunnen til at klokka kan komme til å hoppe tilbake er noe som kalles integer overflow. Dette skyldes hvordan tall lagres i datamaskinen, og da spesielt negative tall. Forklaringen her blir nok litt teknisk, så de minste detaljene får vente til en annen gang, men det er så tilsynelatende enkelt som følgende: Det laveste negative tallet er neste tall i rekken etter det høyeste positive tallet. I alle fall om man ignorerer at den første biten egentlig brukes til fortegn (og dermed skal behandles annerledes). Tallet 011 (3 i det binære tallsystemet) vil da etterfølges av 100 (dvs. 4 i titallssystemet).
Men siden det første sifferet her signaliserer fortegn, vil vi ikke få 4, men heller -4. Det er den laveste verdien vi kan vise med disse tre sifrene (vi har da 8 mulige verdier, fra -4 til 3). Neste tall etter -4 igjen er -3, som derimot er 1 høyere som forventet. Så essensen er altså at når det underliggende binærtallet økes med 1, men allerede er så høyt som det kan bli, kan det altså resultere i at verdien endres til andre enden av skalaen.
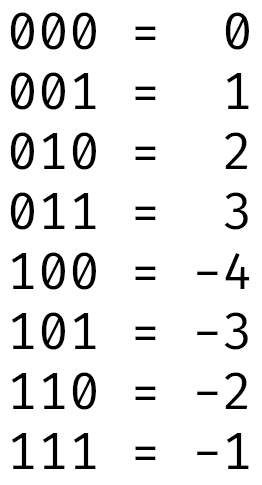
Fikse
Du skulle kanskje tro at det bare var å begynne å lagre datoen med en annen datatype, en som kan lagre større tall? For eksempel med 64 bit, som gjerne er det neste naturlige steget opp. Det vil gi en 4 294 967 296 ganger så høy maksverdi. Da blir høyeste tall 9 223 372 036 854 775 807, eller 9 milliarder milliarder. For hver ekstra bit kan man nemlig lagre dobbelt så mange verdier. Med 64 bit vil man kunne lagre datoer flere hundre milliarder år framover i tid.
I teorien vil dette være en super løsning, men selvfølgelig er ting sjelden så lett. Haugevis av programmer som forventer å få tiden lagret med 32 bit vil ikke kunne takle å plutselig få den med 64 bit. Og hva skjer om et program som forventer tid i 32 bit prøver å regne med en dato etter 2038? Disse kan jo bare lagres om man f.eks. bruker 64 bit. Uansett hvordan man gjør det kommer man ikke unna at datoen blir feil.
Heldigvis har man litt flaks: som nevnt tidligere har i alle fall i programmeringsspråket C egentlig definert lagringen av tid som datatypen «long», eller den fulle formen «signed long integer». Denne har en størrelse på minst 32 bit. På operativsystemer laget for 64-bits prosessorer kan datatypen altså egentlig være på 64 bit. Alle 64-bits programmer vil forvente at det er slik og håndtere det uten problemer. Det er slik Y2K38 løses på 64-bits utgaver av Linux, macOS og andre operativsystemer i Unix-familien. Lignende løsninger for å gå over til 64-bit brukes for Windows også.
Oppsummering
Men enten det nå er på denne måten eller en annen, de fleste operativsystemer har i en årrekke arbeidet med å sørge for å bruke 64 bit for å lagre dato. I alle fall for 64-bits prosessorer, hvor dette stort sett er problemfritt. Og arbeidet har fortsatt for å finne gode løsninger også for 32-bits prosessorer, selv om det inkluderer mer arbeid og større endringer enn for 64-bits. Blant annet er det mer utfordrende å beholde kompatibilitet med eksisterende programmer, som jeg var innom tidligere. Men dette er viktig arbeid, for det finnes mange integrerte systemer som bruker små og billige 32-bits prosessorer. Trolig kommer en god del av disse til å eksistere i et par tiår til.
I teorien er man altså i stor grad klar for Y2K38, for mye forberedelser er allerede gjort. Med fortsatt 16 år igjen i skrivende stund, er det sannsynlig at mange eldre systemer som ennå ikke er fikset enten vil bli oppdatert eller tatt ut av bruk. Men man kan aldri helgardere seg når det gjelder slike ting, og det vil garantert bli merkbare konsekvenser. Så får man bare håpe at man med kontinuerlig innsats for å fikse resterende systemer kan unngå de ødeleggende virkningene som kallenavnet «Epochalypse» kan antyde.
Hva synes du om denne forklaringen av Y2K38-problemet, og tilsvarende lengre forklaringer? Er dette noe du vil ha mer av? Noe jeg forklarte bra eller dårlig? Tilbakemelding, tips og ideer er velkomne enten som en kommentar under, via kontaktskjemaet eller på sosiale medier.
Lyst til å lese flere forklaringer av tekniske konsepter og temaer? Sist forklarte jeg hva HTTPS er, og hvorfor det er en svært viktig del av det moderne internettet. Tidligere har jeg også skrevet om fingerprinting, som er en mye brukt teknikk som lar nettsider spore aktiviteten din på nettet. Er du på leting etter annet innhold kan jeg også anbefale serien med korte tips, hvor du nok finner mye nyttig.
